1. 트리 탐색
① 트리 순회
- 트리 내의 모든 노드를 오직 한 번씩 방문하는 방법 -> 전위 순회/ 중위 순회/후위 순회
②전위 순회

③ 중위 순회

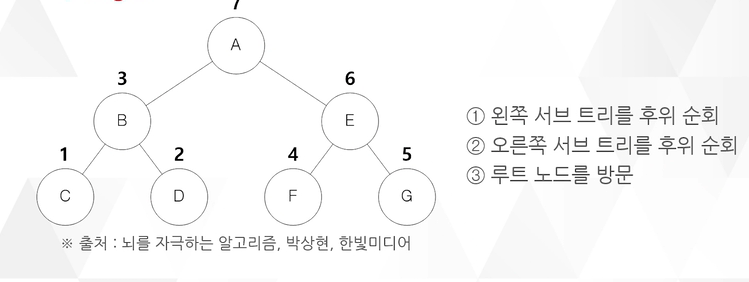
④ 후위 순회
2. 너비 우선 탐색 (큐 이용)
① 그래프 순회
- 하나의 정점에서 시작하여 그래프에 있는 모든 정점을 한번씩 방문하여 처리하는 연산
- 트리 순회와 달리 일반적인 그래프 순회에서는각 정점들을 한 번 이상 방문하는 경우도 있음
- 그래프에서는 다른 모든 정점들을 연결시켜주는 트리의 루트 같은 정점이 존재하지 않을 수도 있음.
② 그래프에서 모든 정점 방문하기
- 임의의 정점 선택하여 탐색하는 방법보다는 시작점을 기준으로 일정한 방향으로 탐색하는 것이 효율적
- 너비우선 탐색 / 깊이 우선 탐색
③ 너비 우선 탐색
- 노드들을 동심원의 형태로 방문하는 것
- 너비 우선 탐색은 결과적으로 동심원의 형태로 차례로 퍼져나가면서 노드를 방문해 가는 형태임.



- 그래프에서 각 정점을 처음으로 방문할 때 사용한 간선들만 남기면 트리가 되는데 이 트리를 너비 우선 트리라고 함
④ 너비 우선 탐색의 장단점
- 장점
> 출발 노드에서 목표 노드까지의 최단 길이 경로 보장
> 각 노드에 대한 최단 경로의 길이 구할 수 있음.
- 장점
> 경로가 매우 길 경우에는 탐색 가지가 급격히 증가하며 많은 기억 공간 필요로 함.
3. 깊이 우선 탐색 (스택 이)
① 깊이 우선 탐색
- 시작 정점의 한 방향으로 갈 수 있는 경로가 있는 곳까지 깊이 탐색
- 더 이상 내려갈 수 없으면 위로 되돌아오다가 내려갈 곳이 있으면 즉각 내려감
- 이진 트리의 inorder, preorder,postorder는 모두 깊이 우선 탐색임.



- 각 정점을 방문할 때 사용한 간선들로 만들어진 트리를 깊이 우선 트리라고 함.
② 장점
- 현 경로상의 노드들만 기억하면 되므로 저장 공간의 수요가 비교적 적음
- 목표 노드가 깊은 단계에 있을 경우 해를 빨리 구할 수 있음
③ 단점
- 해가 없는 경로에 깊이 빠질 가능성이 있음
- 목표에 이르는 경로가 다수인 문제에 대해 깊이 우선 탐색은 해에 다다르면 탐색을 끝내버리므로
이 때 얻어진 해는 최적이 아닐 수 있음.
'CS공부 > 학점은행_알고리즘' 카테고리의 다른 글
| 11-1 위상 정렬 (0) | 2023.08.30 |
|---|---|
| 10-2 최소 신장 트리 (0) | 2023.08.23 |
| 9-2 오일러 사이클과 해밀턴 사이클 (0) | 2023.08.15 |
| 9-1 그래프 개념 (0) | 2023.08.15 |
| 6-1 해시 테이블 개요 (0) | 2023.07.25 |