1. 이진 탐색 트리의 탐색, 삽입, 삭제 연산
① 이진 탐색 트리
- 이진 트리를 탐색용 자료구조로 사용하기 위해 원소 크기에 따라 노드 위치를 정의한 것
② 이진 탐색 트리의 탐색 연산

③ 이진 탐색 트리의 삽입 연산
- 탐색 연산 수행 : >>삽입할 원소와 같은 원소가 트리에 있으면
삽입 불가하므로 같은 원소가 트리에 있는지 탐색하여 확인
>>탐색에서 탐색 실패가 결정되는 위치가 삽입 위치가 됨.
- 탐색 실패한 위치에 원소 삽입

④ 이진 탐색 트리의 삭제 연산
- 탐색 연산 수행: >> 삭제할 노드의 위치를 알아야 하므로 트리 탐색
- 탐색 성공한 위치에 원소 삭제: >> 노드의 삭제 후에도 이진 탐색 트리 유지해야 하므로
삭제 노드의 경우에 대한 후속 처리(이진 탐색 트리의 재구성 작업)가
필요함
- **삭제할 노드가 자식노드를 두개 가진 경우(차수=2)의 삭제 연산
> 노드를 삭제하면, 자식 노드들은 트르에서 연결이 끊어져서 고아가 됨
> 후속 처리 : 삭제한 노드의 자리를 자손 노드들 중에서 선택한 후계자에게 물려줌.
> 후계자 선택 방법
-왼쪽 서브트리에서 가장 큰 자손노드 선택
- 오른 서브트리에서 가장 작은 자손노드 선택

2. 균형 이진 탐색 트리와 AVL 트리의 개념
① 균형 이진 탐색 트리의 개념
- 이진탐색 트리에서 좌우 균형이 잘 맞으면 탐색의 성능이 높고,
이 성능은 탐색 트리의 높이와 밀접한 상관이 있음.
- 왼쪽 서브트리의 높이와 오른쪽 서브트리의 높이에 대한 균형 조건을 추가하여 정의한 트리를
균형 이진탐색트리 or 균형 트리라고 함
②AVL 트리의 개념과 유형
- AVL 트리는 대표적인 균형 이진 탐색 트리
- 각 노드에서 왼쪽 서브 트리의 높이(hL)과 오른쪽 서브 트리의 높이(hR)의 차이가 1 이하인 트리
- 특징 : (hL-hR) : 노드의 균형 인수(BF) ={-1, 0, 1}
③ AVL 트리에서 발생하는 불균형
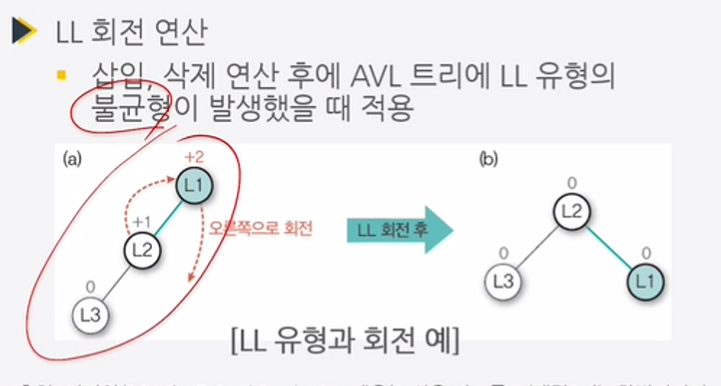
- LL 유형 : (Left-Left 유형)
>> 왼쪽으로 치우쳐 져서 균형이 깨짐(왼쪽 서브트리가 문제)
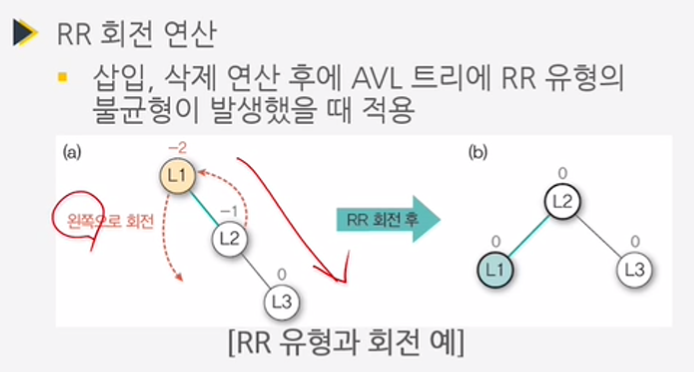
- RR 유형 : (Right-Right 유형)
>> 오른쪽으로 치우쳐 져서 균형이 깨짐(오쪽 서브트리가 문제)
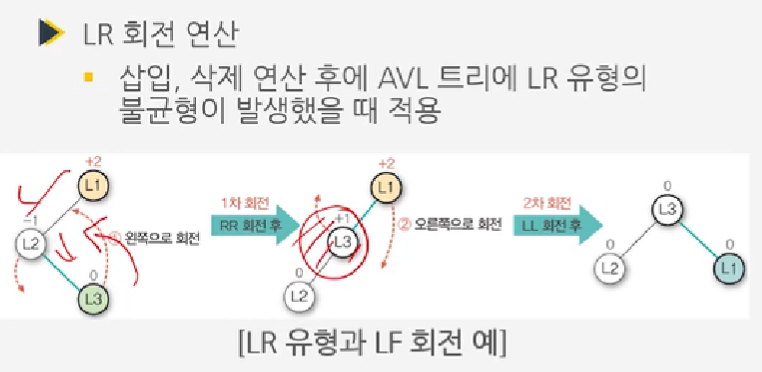
- LR 유형 : (Left-Right 유형) - 왼쪽 서브트리 치우침
- RL 유형 : (RIght-Left 유형) - 오른쪽 서브트리 치우침
2. AVL 트리의 회전 연산 개념
① AVL 트리의 회전 연산
- AVL 트리에서 수행하는 삽입, 삭제 작업은 이진 탐색 트리에서 삽입, 삭제 작업과 같고,
이후에 균형을 맞추어주는 재구성 작업이 추가되는데 이 작업은 회전 연산을 통해 이루어짐.



'CS공부 > 학점은행_자료구조' 카테고리의 다른 글
| 12-1 그래프의 구조 (0) | 2023.09.12 |
|---|---|
| 11-2 히프 개념과 연산 (0) | 2023.08.30 |
| 10-2 이진 트리 순회의 개념 (0) | 2023.08.23 |
| 10-1 트리와 이진트리 (0) | 2023.08.23 |
| 9-2 연결 큐와 데크 (0) | 2023.08.16 |