1. 그래프의 활용
① 가중치 그래프
- 그래프의 정점을 연결하는 간선마다 일정한 값을 할당한 그래프
- 간선에 할당하는 값은 각 정점 간의 거리나 비용과 같은 속성이 할당될 수 있음.
- 그래프 G=(V,E)에서 각 간선에 가중치(Weight)를 부여한 그래프를 의미
2. 최단 경로 문제
① 최단 경로
- 두 정점 사이에 존재하는 여러 경로 중 가중치의 합이 가장 짧은 경로
② 최단 경로 문제
- 다양한 경로들 중 가장 효과적이고 경제적인 경로를 찾는 문제
- 출발점~도착점 경로에 포함되는 정점 나열하고 각 간선에 부여된 가중치를 더하야 가장 작은 가중치의 합을 갖는 경로 선택해 가는 것
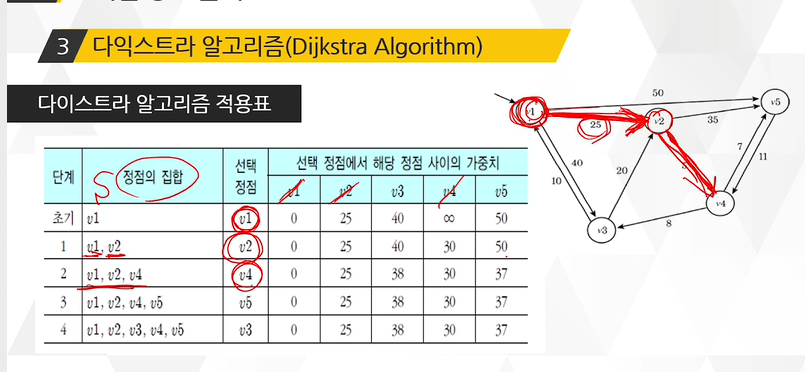
③ 다익스트라 알고리즘
- 시작점으로부터 최단경로 갖는 정점들을 차례로 탐색해 가는 알고리즘.
- 한 정점에서 다른 모든 정점 간의 최단경로를 구함. (각각의 정점으로 갈 때의 최단경로)
- 시작 정점은 거리를 0으로, 다른 모든 정점은 거리를 무한대로 하여 시작
- 거리가 최소인 정점을 선택하고 이것에 인접한 정점의 거리를 최단 거리로 변경하는 과정 반복
3. 경로의 존재
① 경로의 존재
- 정점 v1과 v2를 연결하는 간선 <v1,v2>가 존재한다면 v1에서 v2로 가는 길이가 1인 경로가 있다는 의미
- E¹ :길이가 1인 경로
- E² : 길이가 2인 경로
② 도달 행렬
- 방향 그래프에서 정점 간 경로의 존재 여부를 행렬로 표현한 행렬
- 어떤 한 정점에서 우회하여 갈 수 있는 경로까지 포함하여 경로가 존재하는 지 여부를 판단할 때 사용하는 행렬
③ 플로이드 와샬 알고리즘
- 그래프에서 모든 정점 사이의 최단 거리를 구하기 위한 알고리즘
- 모든 정점에서 모든 정점으로의 최단거리를 구하는 것
- cf) 다익스트라 알고리즘은 어느 한 지점으로부터 모든 정점으로의 최단 거리를 구함
- 한 정점에서 목적지 정점까지의 거리가 다른 정점들을 거쳐서 가는 가중치보다 크다면 거쳐서 가는 거리값을 저장해 나가는 방법

④ 이행폐쇄
- 거쳐서 갈 수 있는 모든 곳을 직접 가는 간선으로 연결한 그래프
- 간선의 추가를 통해서 대부분의 노드들이 인접 노드로 바뀌게 되며 인접행렬로 표현하는 것이 편리

⑤ 그래프 탐색
- 그래프의 연결된 모든 정점을 탐색하기 위해서는 임의의 정점을 선택하여 탐색하는 방법보다 시작점을 기준으로 일정한 방향으로 탐색하는 것이 효율적
- 깊이우선탐색
`

- 너비우선탐색
: 시작 정점을 방문한 후에 시작 정점에 인접한 모든 정점들을 우선 방문함.

'CS공부 > 학점은행_이산수학' 카테고리의 다른 글
| 10-2 트리의 순회 및 이진 탐색 트리 (0) | 2023.08.23 |
|---|---|
| 10-1 트리 (0) | 2023.08.22 |
| 9-1 그래프의 종류 (0) | 2023.08.08 |
| 7-1 그래프의 개념 (0) | 2023.07.25 |
| 6-1 부울 대수 (0) | 2023.07.23 |