1. 트리의 순회
① 트리의 순회
- 모든 노드의 데이터를 처리할 수 있도록 한번씩 방문하는 방법
② 이진 트리 순회
- 일정한 규칙에 따라 이진 트리의 모든 정점을 꼭 한번씩 방문하는것
- 전위 순회, 중위 순회, 후위 순회
- 전위 순회 : 루트를 가장 먼저 순회 -> 왼쪽 부분 트리 -> 오른쪽 부분 트리
- 중위 순회 : 왼쪽 부분 트리 -> 루트를 가장 먼저 순회 -> 오른쪽 부분 트리
- 전위 순회 : 왼쪽 부분 트리 -> 오른쪽 부분 트리 -> 루트를 가장 마지막에 순회 ㅇㅇㅇ
③ 이진 트리의 수식 표현
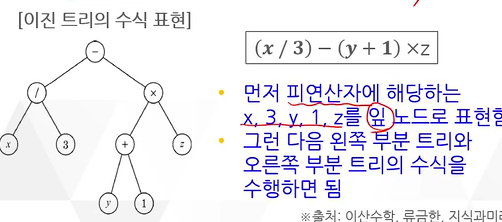
- 연산자와 피연산자가 표현된 수식은 전위표기법, 중위표기법, 후위표기법으로 나타낼 수 있다.
- 전위 표기법 : 연산자와 연관된 2개의 피연산자가 앞에 위치하도록 표기
- 중위 표기법 : 연산자가 연관된 2개의 피연산자 사이에 위치하게 표기
- 후위 표기법 : 연산자가 연관된 2개의 피연산자 뒤에 위치하도록 하는 표기

- 연산자 우선순위에 따라 적힌 것이기 때문에 괄호가 필요없음! > 복잡한 수식일 때 아주 간단하게 연산할 수 있음.
2. 이진 탐색 트리 (탐색시 유!)
① 이진 탐색 트리
- 임의의 정점의 좌측 부분 트리에는 해당 정점보다 작은 값의 데이터들이 높이고 우측 부분 트리에는,
더 큰 값들이 오도록 구성.
- 탐색은 항상 루트에서 시작하여 크기 관계에 따라 좌측 또는 우측 자식을 따라가면서 이루어짐.
- 데이터의 삽입, 삭제가 간단하고 특정 키값을 빠르게 찾을 수 있음.
- 정의 : 이진 트리에서 모든 노드가 키값을 가지고 있으며 키들이 다음의 속성을 만족할 때,
주어진 이진 트리를 이진 탐색 트리라 함.

② 이진 탐색트리에서의 탐색
- 루트에서 시작됨.
- 루트 == 찾으려는 데이터 -> 탐색 종료
- 루트 < 찾으려는 데이터 -> 오른쪽 부분트리 탐색
- 루트> 찾으려는 데이터 -> 왼쪽 부분트리 탐색
- 만약 단말 노드에 이를 때까지 같은 데이터를 찾지 못하면 탐색에 실패하는
3. 신장 트리
① 신장 트리
- 그래프 내의 모든 정점들을 포함하는 트리 (사이클을 포함해서는 안됨)
- 임의의 그래프에서 만들 수 있는 신장 트리는 매우 다양함.
- 최소 신장 트리 : 가능한 신장 트리 중에 간선의 가중치 합이 최소인 신장 트리
'CS공부 > 학점은행_이산수학' 카테고리의 다른 글
| 11-2 계수법칙과 순열 (0) | 2023.08.29 |
|---|---|
| 11-1 최소 신장 트리 (0) | 2023.08.28 |
| 10-1 트리 (0) | 2023.08.22 |
| 9-2 그래프의 최단 경로 (0) | 2023.08.15 |
| 9-1 그래프의 종류 (0) | 2023.08.08 |