puravida

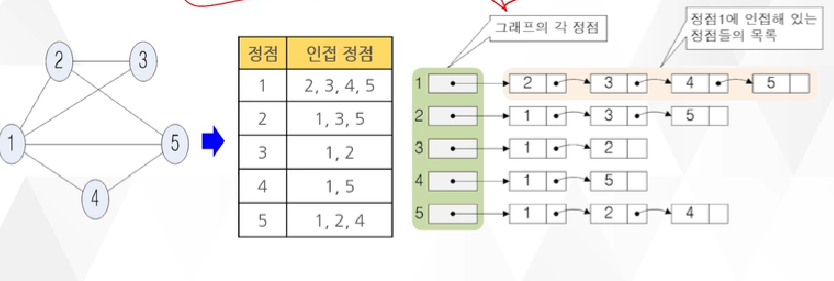
1. 오일러 사이클 (간선 탐색 방법) ① 그래프 이론 : 유한개의 정점과 간선의 결합 방법에 대한 이론 ② 해밀턴 문제 - 12면체 20개의 각 정점에 도시 이름을 적고 어느 한 도시에서 출발하여 모서리를 따라서 다른 모든 19개 도시 방문하고 처음 출발한 도시로 돌아오는 게임 - 각 도시는 단 한 번만 방문 가능 ③오일러 사이클 - 2개의 섬과 7개의 다리로 구성된 공원에서 7개의 다리를 모두 지나가는데 이미 지나갔던 다리는 다시 거치지 않고 갈 수 있는 전체 경로를 해결하는데 오일러는 그래프 이론 사용. - 오일러는 이 문제를 해결하는데 각 정점에 연결된 간선의 개수가 모두 짝수일때만 가능함을 증명 - 각 간선을 정확하게 한번씩만 경유해서 그래프의 모든 간선을 지날 수 있는 경로가 존재하고, 출발 ..

1. 그래프 개념 ⓛ 그래프 - 현실세계의 복잡한 작업을 시각적으로 구조화하여 표현 - 두 정점이 간선으로 연결되어 있으면 인접(Adjacent)하다고 함. - Graph G = (V,E) V: 정점 집합, E: 간선 집합 ② 그래프의 기원 - 오일러가 쾨니히스베르트 7개 다리 문제 풀기 위해 고안한 수학적 도구 ③ 그래프의 예 - 무향 그래프 : 간선에 방향성이 없는 그래프 - 유향 그래프 : 간선이 방향성이 있는 그래프 - 가중 그래프 : 그래프의 정점을 연결하는 간선마다 일정한 값을 할당한 그래프 2. 그래프의 용어 ① 인접(Adjacent) - 간선으로 연결되어 있는 두 정점을 일컫는 말 - 이웃관계 ② 경로(Path) - 그래프에서 간선을 따라 갈 수있는 길을 순서대로 나열한 것 ③ 차수 - 그..

1. 해시 테이블의 개념 - 데이터를 한 번에 찾아줄 수 있는 개념 ① 저장과 검색의 복잡도 - 원소가 저장될 자리가 원소의 값에 의해 결정되는 자료구조 - 저장된 자료와 비교하여 자리를 찾지 않고 단 한번의 계산으로 자신의 자리 찾음 - 평균 O(1) ② 해싱 - 해시 함수를 이용하여 레코드가 저장되어 있는 주소를 직접 구하여 검색 - 키를 비교하지 않고 계산에 의해 검색하는 방법 - 매우 빠른 응답을 요하는 응용에 유용 ex) 주민등록 시스템 ③ 해시 테이블 - 키값과 value 데이터 가진 구조 - 최소 원소를 찾는 것과 같은 작업은 지원하지 않음. - 한 개 이상 보관하는 버킷들의 집합 - 한 개의 버킷에는 하나 이상의 레코드 수용 가능 - 키값을 해시 함수에 넣어서 계산하면 해시 테이블의 주소 ..

1. B-트리 ① B-트리 - 이진 트리 확장하여 하나의 노드가 가질 수 있는 자식 노드의 최대 숫자가 2보다 큰 트리 구조 - 하나의 노드에 많은 수의 데이터가 배치 ② 다진검색트리 - 키가 k개 있으면 k+1개 자식 가짐. - 루트를 제외한 모든 노드는 k/2~k 개의 키를 가짐. - 모든 리프 노드는 같은 깊이 가짐. - 균형을 위해 최대 허용량의 반 이상의 키는 채워야 하는 검색 트리 2. B-트리에서 삽입 3. B-트리에서 삭제 ① 삭제 과정 - x 를 키로 갖는 노드 탐색 - 리프 노드가 아니면 x 직후 원소 y를 가진 리프 노드 r 찾아 x,y바꿈 - 리프 노드 x 제거 - x제거 후 노드에 언더 플로우가 발생하면 적절히 해소 ② 예시

1. 레드 블랙 트리 ① 레드 블랙 트리 - 이진 탐색 트리에 균형을 맞추는 기능을 추가한 트리 : 삽입/삭제가 일어나는 경우, 높이 작게 유지하는 자가 균형 이진트리 - 리플 노드들이 비어있고, 자료를 가지고 있지 않음. - 순수 이진 탐색 트리에서는 한쪽으로 치우친 사향 이진 트리의 경우 탐색 효율이 극도로 떨어지고, 레드 블랙 트리는 균형이 잡히므로 이진 탐색 트리에 비해 효율적이다. ② 레드 블랙 특성 - 이진탐색 트리 조건 + 레드 블랙 특성 만족해야 함. - 각 노드는 레드나 블랙/ 루트는 블랙 - 모든 리프(NIL 노드)는 블랙 *여기서 리프노드는 자료 가지지 않고 트리의 끝 나타내는 것 의미 - 레드 노드의 자식 노드 양쪽은 모두 블랙(레드는 연속적으로 안나타남) - 루트 노드에서 임의의 ..

1. 관계의 개념 ① 관계 - 서로 다른 집합에 있는 원소들 사이의 관련성 - 이항 관계 : 집합 X에서 집합 Y로의 R은 X x Y의 부분집합 ② 곱집합 - 집합 A,B의 곱집합 AxB는 A,B의 원소의 모든 순서쌍 2. 관계의 표현 ① 화살표 도표 ② 부울행렬 - 관계존재 시 1, 존재 안할 때는 0 3. 관계의 성질/역관계/합성관계 ① 관계의 성질 -반사성, 대칭성, 추이 ② 역관계 : 관계 R이 존재할때 R-1 만들 수 있음 - 관계 R의 정의역은 R-1의 치역이 되고 관계 R의 치역은 R-1의 정의역이 된다. - 관계 R의 순서쌍의 앞,뒤 원소를 바꾸면 역관계가 되어 R-1을 나타냄 ③ 합성관계 - R₁은 A->B 관계이고, R₂는 B->C관계일 때 R₂ · R₁는 R₁을 적용한 후 R₂를 적용..

1. 이진 탐색 트리 ① 이진 탐색 트리 - 데이터 삽입, 삭제, 탐색 등이 자주 발생하는 경우 효율적인 구조 - 이진 트리이면서 같은 값을 갖는 노드가 없어야 함. - 탐색, 삽입, 연산 평균적 시간복잡도 : O(logn) -트리의 높이 ② 이진 탐색 트리에서의 탐색 - 데이터 탐색은 루트에서부터 시작 - if루트 != 찾으려는 데이터: if루트 노드 데이터 찾고자 하는 데이터: go 왼쪽 ③ 이진 트리 탐색에서 재귀적 관점 - 루트 노드 t에서 왼쪽 자식 Left[t]로 분기하는 것은 Left[t]가 새로운 루트가 되었을 뿐 앞의 과정과 똑같은 작업( 재귀적) 2. 이진 탐색 트리에서 삽입 ① 데이터 삽입 - 탐색 성공시, 삽입은 실패..

1. 레코드, 키의 정의 및 탐색 트리 ① 탐색 - 기억 공간에 보관 중인 데이터 중에서 원하는 정보를 찾아내는 작업 - 순차 탐색, 이진 탐색 등이 있다. - 적절한 자료구조와 알고리즘의 사용은 효율적인 데이터의 저장과 탐색에서 매우 중요함. - 배열의 경우 데이터가 들어오는 순서대로 쌓아서 저장은 쉽지만, 검색이 번거로움. ② 레코드, 키, 탐색트리 - 레코드 : 개체에 대해 수집된 모든 정보를 포함하고 있는 저장 단위 (행 전체) - 필드 : 레코드에서 각각의 정보를 나타내는 부분(열) - 키 : 다른 레코드와 중복되지 않도록 각 레코드를 대표할 수 있는 필드(ex. 사원번) 키는 필드 하나로 구성할 수도 있고, 두 개 이상의 필드로 구성할 수 있음. - 탐색 트리 : 각 노드 가 규칙에 맞도록 하..

1. 힙정렬 ① 힙정렬 - 주여진 배열을 힙으로 만든 후 차례로 하나씩 제거하며 정 ② 힙 정렬 방법 - 주어진 배열을 힙으로 만든 후 가장 작은 값부터 제거하며 힙의 크기 줄여나감. - 정렬은 힙에서 원소들이 제거된 순서대로 함. - 힙에서 최소원소를 제거하고 나서 힙 성질을 만족하도록 수선해주는 과정이 필요 ③ 힙 정렬의 작동 예 - 맨뒤에서 부터 따져서 힙 성질에 문제가 생길 수 있는 지 체크함. - 루트 노드의 원소를 제거하여 다른 곳에 저장하면서 저장 ④ 힙정렬 알고리즘 heapSort(A[],n) #A[1...n]을 정렬한다 { buildHeap(A,n); #힙 만들기 for i 빠름 - 기수 정렬 시간: O(n) ② 기수 정렬 방법 - 정렬하고자 하고자 하는 숫자들을 가장 낮은 자리수 가지고..

1. 쉘정렬 ⓛ 쉘정렬 - 주어진 입력 데이터를 적당한 매개 변수의 값만큼 서로 떨어진 데이터들과 비교하여 교환하는 과정을 매개변수의 값을 바꾸어가며 되풀이하는 것. - 매개변수를 계속 줄여가다가 1(간격)이되면 종료. => 모든 원소를 1개 그룹으로 여길 때(삽입 정렬) end! ② 쉘 정렬 복잡도 - 쉘 정렬 최악의 경우 시간복잡도 O(n²)--> 간격 선정에 따라 좌우됨 ③ 쉘 정렬의 특징 - 임베디드 시스템(가전제품의 프로그램)에 주로 사용(입력크기가 매우 크지 않은 경우에 성능이 좋음). 2. 병합 정렬 ⓛ 병합정렬(Merge Sort) - 정렬할 데이터들을 2개로 나누고 각각 정렬한 후에 다시 병합하여 정렬 완성 mergeSort(A[],p,r) { if (p